In each year of a model run, the network will have either a net funding requirement or a cash surplus, based on the accumulation of revenue, investment and costs, together with interest, tax and short-term changes in working capital. STEM lets you control the source of funding for the network and the disposal of any surplus cash.
The two primary sources of funding for investment in a telecoms network are long-term borrowing (debt) and share capital (equity), and the gearing between these forms the heart of the financial model in STEM, which is described in detail in the following pages.
The profit and loss and cashflow statements and the balance sheet, together with the underlying equations, are all described in 10.3.14 Financial statements.
Long-term borrowing
In reality, most long-term borrowing is made up of a number of separate loans or bonds, some of which will have fixed repayment schedules. We considered modelling individual loans and bonds within STEM, but the complexities and variety of such arrangements were felt to be inappropriate for a STEM model, and so a single Borrowing Rate governs the calculation of interest on long-term borrowing, and should be set to reflect the average cost of borrowing in the particular business you are modelling.
Borrowing payable proportion
The amount of long-term borrowing which must be re-paid in the coming year should be shown as a short-term liability on a balance sheet, but in the absence of detail regarding individual loans this cannot be calculated directly. Instead a time-series input specifies Borrowing Payable as a proportion of Long-Term Borrowing. For example, if the loans and bonds in the business you are modelling have an average repayment schedule of five years, it would be appropriate to set this proportion to 0.2; but care should be taken where the level of borrowing is increasing significantly from one year to the next, as the money borrowed five years ago will make up rather less than 20% of the total borrowing under these circumstances.
Share capital
Funds raised by issuing shares in a business have two main differences from long-term borrowing. Firstly shareholders are the owners of the business: if the business fails, all long-term borrowing is re-paid before compensating the shareholders. Secondly the return on this investment is paid as dividends, linked directly to the profitability of the company, rather than as interest on the sum invested.
Again in the real world, companies sometimes issue several classes of share, such as preference shares, with different rules regarding creditor status and eligibility to dividends; but this was also felt to be superfluous to the issues in a STEM model.
Gearing
When STEM calculates a net funding requirement for a model (essentially by comparing the written-down value of assets plus working capital with cumulative retained profit), this sum will be matched with a combination of long-term borrowing and new share capital, calculated to match a Target Gearing which you specify as a time-series input.
The gearing is ‘net of cash’ and is defined as:
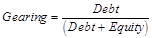
where
Debt = Long-Term Borrowing + Overdraft – [all forms of] Cash
Equity = Share Capital + Retained Earnings.
In the real world, it is unusual for the share capital in a business to decrease, so the specified gearing is taken as a constraint. Thus, in our model, the share capital cannot decrease. If there is already more share capital than required by the desired gearing, borrowing will be correspondingly reduced, resulting in an actual gearing lower than originally specified.
Dividends
Dividends are calculated as a proportion of profit after interest and tax. However, it is commonplace for dividends to be paid either wholly or partly in arrears, and so a time-series input is provided which allows you to specify what proportion, if any, should be paid as interim dividends in the current year – see 10.3.11 Financial charges: interest, tax and dividends.
Tax
Tax is calculated as a proportion of profit after interest, with some scope for tax relief for prior losses. In line with the calculations for dividends, a time-series input allows you to specify what proportion of tax, if any, should be paid in the current year – see 10.3.11 Financial charges: interest, tax and dividends.
Current account
Regardless of whether a network has a net funding requirement or cash surplus, it will always need a certain level of cash in the ‘current account’ in order to service its day-to-day financial requirements, significant because it will not earn interest. A time-series input, Average Cash Days, specifies the number of days Operating Costs which should be in the current account.
Note: Operating Costs does not include capital costs (unlike the Operating Expenditure and Operating Charge results), which reflects the fact that capital investment is usually planned, and does not affect the current account.
Note: This explicit necessity for cash in the current account means that a little borrowing might be necessary even if there is a marginal cash surplus.
Overdraft
If you want to record an overdraft in the balance sheet, you can specify a negative number for the Average Cash Days input described above. Rather than show negative Cash, a separate Overdraft result is given, but of course only one of these will be non-zero. An Overdraft Rate is provided in order to calculate the corresponding interest.
Surplus cash
If there is a net cash surplus which exceeds the requirements of the current account, the network is free to invest the remaining cash. By default, all surplus cash earns interest at the Deposit Rate. In reality there may be a mix of short-term investments (typically marketable securities) and long-term investments (such as long-term bonds or strategic investments in other companies). While it would be impractical to model individual investments, a time-series input, Long-Term Investment Proportion, allows you to specify long-term investment as a proportion of surplus cash. An Investment Rate is also provided to govern interest earned on long-term investment.
Interest
In earlier versions of STEM (prior to 5.3), interest was calculated on the average cash balance over the year, taking into account the interest itself, which allowed for a simple, closed formula. Either the Borrowing Rate or Deposit Rate was used, according to the sign of the average balance.
Now that we keep a separate record of Long-Term Borrowing, Overdraft, Cash Deposits and long-term Investments, each of the interest rates is simply applied to the respective average balances over the year. However, the downside of these intricacies is that it is no longer possible to produce a closed formula for the interest, and consequently, for the final balances. Since the interest expense and income affect the retained profit, the calculations for the entire balance sheet become circular, and have to be resolved through iteration – see
4.12.4 Using iteration to resolve circular references. Since the interest rates are constrained to be less than 1, the movement of the balances should reduce exponentially with each successive iteration, and thus converge. Furthermore the solution is guaranteed to be unique by the essential linearity of the equations.
Note: Whilst it is theoretically possible to produce a closed formula for the net interest from each of the separate equations, the analysis is complicated enormously by the fact that you have to cater for a number of different cases, depending on whether the network is in profit, whether there is any slack in the gearing constraint, and so on. It is likely that you would have to try a different set of formulae for each hypothetical outcome in order to establish which provided a consistent set of values. This approach would be very sensitive to any subsequent extensions we might make to the financial model, and thus less robust than the iterative solution.