The dimensioning of a telecoms system is based on the concept of a number of connections having an intermittent demand for calls that must be distributed on a smaller number of circuits. Although theoretically possible, the provision of the same number of circuits as connections would be uneconomical. In practice, as demand is intermittent and spread across time, a much smaller number of circuits than connections suffices. As the ratio of circuits to connections decreases, the probability that no circuit will be available to satisfy demand increases. If this happens the telephone call will be blocked. This probability is called the Grade of Service (GoS).
Grade of Service
Assuming that telephone calls arise in a random manner, the GoS can be derived mathematically as a function of the demand and the number of circuits:
 (1)
(1)
where
v = level of demand, expressed in Erlangs
m = number of circuits.
Note: The input to an Erlang B Transformation is interpreted as carried traffic, and is scaled up by a factor of 1 / (1 – GoS) to get the offered traffic in order to calculate the number of required circuits.
Traffic unit
The Erlang is a unit of traffic. It represents the total calling demand arising in a given time period. The demand in Erlangs,
v, can be derived from the number of calls during the period and the average call duration:
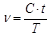 (2)
(2)
where
C = number of calls during the period
t = average call duration
T = length of the time period.
The period T
is the peak-time busy hour, as the number of circuits should be dimensioned to be able to handle the peak-period demand. The busy-hour traffic in Erlangs is calculated from the total annual traffic in call minutes, divided by the number of busy days per year, to derive the average number of call minutes per busy day, and then multiplied by the proportion of traffic falling in the busy hour. This gives the traffic in call minutes falling in the busy hour, which is then divided by 60 to convert to Erlangs.
The proportion of traffic falling in the Busy Hour is a function of the daily traffic pattern in the telecoms system considered, as in the following illustration.
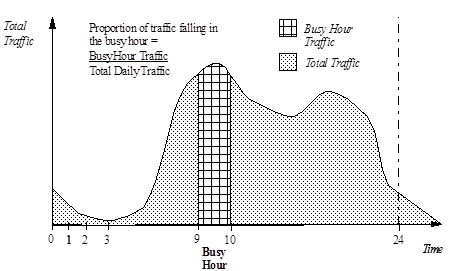
Figure 1: A typical PSTN telecoms system and demand formula
Note: It is assumed that all Services (e.g., Residential/Business) in a model have the same busy hour, which is a conservative assumption as this will tend to over-estimate the required capacity.
For a given GoS and v, the formula (1) is applied iteratively to calculate the required number of circuits, m.
Non-linearity
As the Erlang B formula is highly non-linear, it is important to specify the number of sites (or links) across which traffic, and hence capacity, is distributed, rather than assuming that demand should be treated as one single bundle. The total busy-hour traffic in Erlangs, v, is divided by the number of sites, to derive the demand per site in Erlangs, before applying (1). The number of circuits per site, m, calculated from (1), is then multiplied by the number of sites to derive the total number of circuits required.
Note: This deployment constraint imposed on an Erlang B Transformation is only used for Erlang B calculations and is not passed on to the Resources installed by the Transformation. The geographical deployment of the Resources must be specified separately.
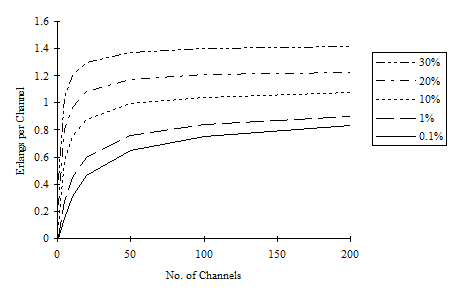
Figure 2: Non-linear Erlang B formula for various Grades of Service
Example
Assume v = 1 Erlang and GoS = 1%. Using (1), five circuits are required to meet this level of demand. If three sites are specified in the Erlang B Transformation, eight circuits must be installed. If the deployment constraint is imposed on the circuit Resource with a Homogeneous distribution, nine circuits are necessary (three circuits per site across three sites).

Figure 3: Erlang B Formula allowing for Deployment